Алгоритм обхода ndfsm
Основная идея алгоритма обхода ndfsm заключается в следующем. Если в недетерминированном графе существует детерминированный сильносвязный полный остовный подграф, то алгоритм движения может использовать этот подграф для построения обхода, не сталкиваясь непосредственно с проблемами недетерминизма.
Ориентированный граф G' = ( VG', XG', EG' ) называется остовным подграфом ориентированного графа G = ( VG, XG, EG ), если VG' = VG, XG' = XG и EG'

Остовный подграф G' = ( VG', XG', EG' ) ориентированного графа G = ( VG, XG, EG ) называется полным остовным подграфом, если






Напомним, что алгоритмом движения на ориентированных графах называется функция α, которая по ориентированному графу G = ( VG, XG, EG ), текущей вершине v



Пусть e = ( e1, e2, …, en ) - пройденный маршрут в графе G = ( VG, XG, EG ). Тогда мы будем использовать следующие обозначения. Множеством пройденных вершин VGe мы будем называть множество вершин пройденного маршрута:
VGe = { vg




Пройденным подграфом мы будем называть граф G'e = ( VGe, XG, { e1, e2, …, en } ).
Пусть ei = ( vi, xgi, v'i ). Тогда детерминированным пройденным подграфом мы будем называть граф G''e = ( VGe, XG, { ei |




Будем говорить, что стимул xg пройден в вершине vg, если существуют такая вершина vg'


Если в вершине vg все допустимые стимулы являются пройденными, то такая вершина будет называться завершенной.
Для обеспечения детерминированности функции мы будем считать, что множество стимулов XG является фундированным, то есть множество линейно упорядоченно и в нем отсутствует бесконечно убывающая последовательность элементов.
Определение 20.
Алгоритмом движения ndfsm мы будем называть функцию αndfsm, которая по неизбыточному описанию ориентированного графа G = ( VG, XG, π ), текущей вершине v



- Если текущая вершина не является завершенной, то функция возвращает минимальный стимул из π(v), который не является пройденным в текущей вершине;
- Иначе, если в детерминированном пройденном подграфе существует маршрут, ведущий из текущей вершины в какую-либо из незавершенных пройденных вершин, то функция возвращает стимул, приписанный к дуге ei пройденного маршрута, которая обладает минимальным индексом среди всех дуг, являющихся первыми дугами в кратчайших маршрутах детерминированного пройденного подграфа, ведущих из текущей вершины в какую-либо из незавершенных пройденных вершин;
- В противном случае функция возвращает τ.
Корректность определения следует из фундированности множества стимулов и конечности пройденного подграфа.
При работе с недетерминированными графами алгоритм движения не может гарантировать обход всех дуг графа, так как алгоритм не может выбрать конкретную дугу среди набора дуг, начинающихся в одной вершине и помеченных одним стимулом. Этот выбор происходит недетерминированно и независимо от работы алгоритма движения. Поэтому для недетерминированных графов вводится понятие обхода по стимулам, которое совпадает с понятием обхода на классе детерминированных графов и является более слабым на классе недетерминированных графов.
Обходом по стимулам [] конечного ориентированного графа G = ( VG, XG, EG ) называется маршрут v1
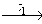
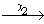
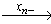


Алгоритм движения α называется алгоритмом обхода по стимулам на классе конечных ориентированных графов Æ, если на любом графе G из класса Æ любое функционирование алгоритма движения α является конечным обходом по стимулам графа G.
Лемма.
Алгоритм движения ndfsm является алгоритмом обхода по стимулам на классе конечных графов, обладающих детерминированным сильносвязным полным остовным подграфом.
Доказательство.
Предположим, что это не так. Тогда существует конечный граф G = ( VG, XG, EG ), обладающий детерминированным сильносвязным полным остовным подграфом, и функционирование e = ( e1, e2, …, en, … ) алгоритма ndfsm на этом графе такие, что e не является конечным обходом по стимулам графа G. Такое может быть в двух случаях: если функционирование e является конечным, но не является обходом по стимулам графа G, и если функционирование e является бесконечным.
1. Предположим, что функционирование e = ( e1, e2, …, en ) является конечным, но не является обходом по стимулам графа G. Тогда из определения функционирования следует, что αndfsm( A, v'n, e ) = τ . Следовательно вершина v'n является завершенной и в детерминированном пройденном подграфе G''e не существует маршрута, ведущего из вершины v'n в какую-либо из незавершенных пройденных вершин.
С другой стороны e не является обходом по стимулам графа G, то есть в графе G существует такая дуга ( v, x, v' )


Рассмотрим детерминированный сильносвязный полный остовный подграф G' = ( VG', XG', EG' ) графа G. Так как подграф является остовным, то обе вершины v и v'n принадлежат VG'. Так как граф G конечный, а его подграф G' - сильносвязный, то существует конечный маршрут f = ( f1, f2, …, fk ), ведущий из v'n в v. Пусть fi = ( wi, yi, w'i ). Тогда для всех i



Следовательно, наше предположение относительно существования второй дуги ( wi, yi, w''i )

Докажем индукцией по пути f = ( f1, f2, …, fk ), что все вершины w'i являются завершенными для i

База индукции . Вершина w1 = v'n

Предположение индукции . Пусть вершина w'i-1 = wi является завершенной.
Шаг индукции . Так как вершина wi является завершенной, стимул yi является допустимым в этой вершине и дуга ( wi, yi, w'i ) является единственной дугой, выходящей из wi и помеченной стимулом yi, то дуга ( wi, yi, w'i ) также является пройденной, то есть ( wi, yi, w'i )

Мы доказали, что все вершины w'i являются завершенными. Следовательно, и вершина w'k = v

2. Предположим, что функционирование e = ( e1, e2, …, en, … ) является бесконечным. Тогда для всех i ≥ 0 αndfsm( A, v'i, ( e1, …, ei ) ) ≠ τ.
Определим функцию βG на графе G, устанавливающую соответствие между маршрутом ( e1, …, ei ) в графе G и парой натуральных чисел (b1,b2), следующим образом:
- b1 равно числу дуг графа G, отсутствующих в маршруте ( e1, …, ei ), |EG \ { e1, …, ei }|;
- b2 равно
- 0, если i = 0, вершина v'i является незавершенной или в детерминированном пройденном подграфе нет маршрута, ведущего из вершины v'i и в какую-либо из незавершенных пройденных вершин;
- минимальной длине маршрута в детерминированном пройденном подграфе, начинающегося в вершине v'i и заканчивающегося в какой-либо из незавершенных пройденных вершин, в противном случае.
Определим на множестве пар натуральных чисел линейный порядок:
(b1,b2) < (b'1,b'2)b1 < b'1 (b1 = b'1
(b1 = b'1 b2 < b'2)
b2 < b'2)
Отметим, что множество пар натуральных чисел с данным линейным порядком образуют фундированное множество, то есть множество, в котором отсутствует бесконечно убывающая последовательность элементов.
Согласно определению βG( () ) = (|EG|,0).
Покажем, что для любого префикса ( e1, …, ei ) функционирования e
βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) )
Для всех i ≥ 0 αndfsm( A, v'i, ( e1, …, ei ) ) ≠ τ. Следовательно, либо вершина v'i не является завершенной, либо в детерминированном пройденном подграфе существует маршрут, ведущий из вершины v'i в какую-либо из незавершенных пройденных вершин.
Рассмотрим первый случай. Если вершина v'i не является завершенной, то αndfsm возвращает минимальный стимул из π(v), который не является пройденным в вершине v'i. На этом основании можно сделать вывод, что ei+1 является дугой, не принадлежащей { e1, …, ei }. Поэтому первый компонент βG( ( e1, …, ei+1 ) ) на единицу меньше первого компонента βG( ( e1, …, ei ) ), откуда следует, что βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ).
Рассмотрим второй случай. Если вершина v'i является завершенной и в детерминированном пройденном подграфе существует маршрут, ведущий из вершины v'i в какую-либо из незавершенных пройденных вершин, то αndfsm возвращает стимул, приписанный к дуге ej пройденного маршрута, которая обладает минимальным индексом среди всех дуг, являющихся первыми дугами в кратчайших маршрутах детерминированного пройденного подграфа, ведущих из текущей вершины в какую-либо из незавершенных пройденных вершин.
При этом дуга ei+1 может либо совпасть c дугой ej, либо нет.
Если дуга ei+1 совпадает c дугой ej, то уменьшается на единицу второй компонент функции βG, так как кратчайший маршрут в детерминированном пройденном подграфе станет на одну дугу короче, или же в результате перехода будет достигнута незавершенная вершина. При этом первая компонента функции βG останется неизменной, поэтому βG( ( e1, …, ei, ei+1 ) ) будет меньше βG( ( e1, …, ei ) ).
Если дуга ei+1 не совпадает c дугой ej, то эта дуга не принадлежит { e1, …, ei }, так как в противном случае дуга ej не была бы частью детерминированного пройденного подграфа. Следовательно первый компонент βG( ( e1, …, ei+1 ) ) на единицу меньше первого компонента βG( ( e1, …, ei ) ), то есть βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ).
Мы показали, что для всех i ≥ 0 βG( ( e1, …, ei, ei+1 ) ) < βG( ( e1, …, ei ) ). Следовательно функционирование e не может быть бесконечным, так как в противном случае последовательность βG( ( e1, …, ei ) ) образует бесконечно убывающую подпоследовательность в фундированном множестве.
Алгоритм движения ndfsm позволяет заменять стандартный алгоритм dfsm, в тех случаях когда отдельные сценарные функции имеют недетерминированную природу, а другие гарантировано обеспечивают детерминированное движение по графу.
Определение 21.
Асинхронным тестовым сценарием ndfsm относительно асинхронной модели требований A = ( V, X, Y, Z, E ) с множеством стабильных состояний VSV и начальным состоянием v0 VS, называется стационарный автоматный тестовый сценарий, в котором в качестве алгоритма движения по графу сценария используется алгоритм обхода αndfsm.
VS, называется стационарный автоматный тестовый сценарий, в котором в качестве алгоритма движения по графу сценария используется алгоритм обхода αndfsm.
Содержание раздела
