Установка взаимосвязи между погрешностями датчиков и конечного звена механизма.

После расчета погрешностей датчиков вернемся к основному уравнению, устанавливающему взаимосвязь погрешностей перемещения конечного звена механизма с погрешностями датчиков (13.1). При наличии избыточного количества датчиков уравнение (13.1) представляет собой систему линейных уравнений, в которой размерность вектора ?R[6 x 1] ниже, чем размерность ?q[n x 1], где n - количество датчиков, n

m. Прежде чем проводить дальнейшие рассуждения, приведем одно замечание. Уравнение (13.1) является исходным уравнением только для анализа погрешностей датчиков и выбора координат , измеряемых данными датчиками, которые следует использовать для вычисления положения конечного звена.

Представим (13.1) в виде

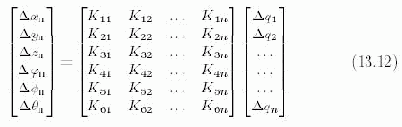
Требуется в (13.12) из матрицы K размерности [6 x 1] выбрать такое сочетание столбцов j=6, которое обеспечивает минимальные погрешности [?xп?yп?zп?

п??п??п]T

min.

Сначала рассмотрим решение указанной задачи для одной из координат вектора ?R. В этом случае анализируется только одна строка в (13.12), соответствующая данной координате. Необходимо выбрать такое сочетание слагаемых в анализируемой строке, чтобы обеспечить |?ri|

min. Задача в такой постановке имеет решение только для заданных значений погрешностей датчиков, потому что при переменных значениях погрешностей имеется множество решений. В качестве регулярных значений погрешностей датчиков может приниматься максимальное либо статическое отклонение. Задача решается в детерминированной постановке и аналогична задаче коммивояжера, когда требуется выбрать минимальный путь (в нашем случае погрешность), проходя через заданное число пунктов (датчиков) из некоторого множества, не повторяя их. Решение выполняется перебором сочетания датчиков по дереву решений (рис. 13.3).

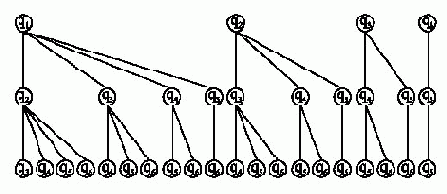
Рис. 13.3.

Вычислив погрешность по каждой из ветвей, выбирается такое сочетание координат, измеряемых данными датчиками, которое обеспечит минимальную погрешность вычисления ?ri. На рисунке 13.3 приведено дерево решений для сочетания датчиков C63=20, где qi - общее количество датчиков (i=1…6), из которых выбираются три информационных.

Выбор информационных датчиков можно осуществить, рассматривая их погрешности как случайные величины по среднеквадратичным отклонениям. В этом случае выполняется задача сортировки слагаемых в анализируемой строке, располагая их в возрастающей последовательности. В качестве информационных датчиков принимаются m датчиков, соответствующих m минимальным слагаемым.

Если требуется выбрать сочетание информационных датчиков, обеспечивая минимальную погрешность по нескольким координатам вектора ?R, то это может быть, например, минимум среднеквадратичного отклонения линейных координат

?п=(xп2yп2zп2)1/2

Как и в предыдущем случае, ?п вычисляется перебором для различного сочетания ?qi и выбирается такое сочетание датчиков, для которого ?п=min.

Особый интерес представляет задача выбора сочетания датчиков при их однотипности, когда погрешность ?qi=const. В данном случае анализируются только коэффициенты матрицы K в (13.12).

Процедура выбора информационных датчиков может выполняться только для линейных или только для угловых координат вектора ?R.

Содержание раздела

Главная сайта