Физические и математические основы оптических систем контроля.
Рассмотрим случай, когда производится контроль геометрических размеров на плоскости, располагаемой перпендикулярно к оптической оси телекамеры (рис. 12.3).
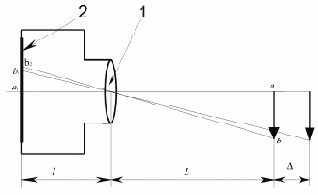
Рис. 12.3.
Изображение, зафиксированное телекамерой, записывается в память компьютера как двумерный массив координат точек анализируемой поверхности в пикселях1).
При определении расстояния между точками на плоскости (рис. 12.3) первоначально определяется масштаб m0 — количество единиц длины, приходящихся на один пиксель. Рассмотрим эталонный отрезок ab длиной A (мм), расположенный на расстоянии L от оптического центра объектива. На фотоматрице телекамеры этому отрезку соответствует отрезок a1b1 длиной B1, измеренный в пикселях. Масштаб определяется отношением
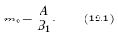
Если отрезок ab сместить на расстояние ? вдоль оптической оси a1a, то согласно правилу подобия получим
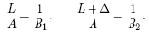
Поделив левые и правые части полученных равенств друг на друга, получим
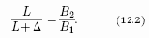
Из (12.2) следует, что взаимосвязь между масштабами при параллельном переносе объекта контроля на расстояние определяется зависимостью
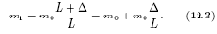
Для определения геометрических размеров анализируемой поверхности используется дифракционная решетка (4, рис. 12.2), которая представляет прозрачную пластину с нанесенными на ней темными полосами (рис. 12.4). Например, решетка, имеющая размер в плане 50x50 мм, расстояние между линиями и их ширину — 1 мм, при точности нанесения линий 1 мкм позволяет на расстоянии L=1,5—2 м выполнять измерение с точностью 6 мкм.

Рис. 12.4.
С помощью дифракционной решетки можно получить полную (непрерывную) информацию о контролируемой поверхности, попадающей в поле зрения фотоматрицы. Точность измерения лимитируется частотой полос эталлонной решетки, которая не должна превышать пяти пикселей фотоматрицы, при этом промежуточные значения, описывающие контролируемую поверхность, получают аналитически.
Теперь, когда понятна общая схема, связанная с фиксацией изображения в телекамере и масштабированием размеров контролируемого изделия, рассмотрим задачу определения границ изделия по перепадам интенсивности света, попадающего на каждый пиксель фотоматрицы.
Основным признаком границы изображения является перепад интенсивности освещения в направлении, перпендикулярном линии, определяющей границу. В силу наличия микронеровностей на поверхности, а также дифракции света, граница всегда будет размыта. Распределение интенсивности света I(n) в направлении, перпендикулярном границе в точке n0 имеет вид, представленный на рисунке (рис.12.5, а). Пунктиром обозначен перепад интенсивности в идеальном случае.
Производная по перемещению n от интенсивности света I(n) на границе (в точке n0) аппроксимируется кривой Гаусса (рис. 12.5, б).

где A — константа, характеризующая максимальное значение перепада интенсивности отраженного света; ? — среднеквадратичное распределение перепада интенсивности отраженного света на границе; n0 — координаты границы.
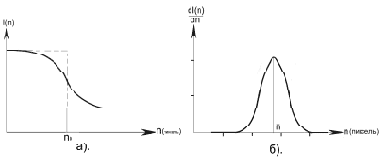
Рис. 12.5.
Для получения распределения интенсивности I(n), зависимой от координат контролируемого изделия, необходимо количество пикселей n умножить на масштаб m0. В этом случае будем иметь распределение интенсивности света, попадающего от контролируемого изделия, в координатах, представленных в системе координат фотоматрицы телекамеры. Следует отметить, что данные координаты будут изменяться с дискретностью, равной масштабу m0, Поэтому измерение расстояний в этом случае будет осуществляться с погрешностью, равной масштабу, что недопустимо для контроля геометрических размеров сложных поверхностей.
Точность определения границ может быть значительно повышена, если интенсивность отраженного сигнала I(r) аппроксимировать функцией, зависимой от непрерывных координат r. При этом координаты, соответствующие максимальному значению перепада интенсивности, определяются дифференцированием непрерывной функции I(r) с более высокой точностью, чем в дискретном случае.
Рассмотрим решение данной задачи для двумерного случая. Перепад интенсивности на плоскости характеризуется модулем градиента функции I(x,,y) от двух переменных x, y
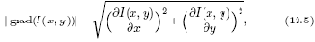
где переменные x и y представляют линейные величины в двух взаимно перпендикулярных направлениях и измеряемые в единицах длины.
