Основы теории анализа и распознавания изображений.
Пусть дано множество M объектов ; на этом множестве существует разбиение на конечное число подмножеств (классов) ?, i = {1,m},M =

Пусть задана таблица обучения (таблица 4.1). Задача распознавания состоит в том, чтобы для заданного объекта ? и набора классов ?1, ..., ?m по обучающей информации в таблице обучения I0(?1...?m) о классах и описанию I(?) вычислить предикаты:
Pi(?




где i= {1,m} , ? - неизвестно.
|
?1 |
 |
 |
 |
?1 | |||||
| ... | |||||||||
|
?r1 |
r11 |
 |
 | ||||||
| ... | |||||||||
|
?rk |
 |
 |
 |
?m | |||||
| ... | |||||||||
|
?rm |
 |
 |
 | ||||||
Рассмотрим алгоритмы распознавания, основанные на вычислении оценок. В их основе лежит принцип прецедентности (в аналогичных ситуациях следует действовать аналогично).
Пусть задан полный набор признаков x1, ..., xN. Выделим систему подмножеств множества признаков S1, ..., Sk. Удалим произвольный набор признаков из строк ?1, ?2, ..., ?rm и обозначим полученные строки через S?1, S?2, ..., S?rm, S?' .
Правило близости, позволяющее оценить похожесть строк S?' и S?r состоит в следующем. Пусть "усеченные" строки содержат q первых символов, то есть S?r=(a1, ..., aq) и S?'=(b1, ..., bq) . Заданы пороги ?1...?q,


|aj-bj|

Величины ?1...?q,

Пусть Гi(?') - оценка объекта ?' по классу ?i.
Описания объектов {?'}, предъявленные для распознавания, переводятся в числовую матрицу оценок. Решение о том, к какому классу отнести объект, выносится на основе вычисления степени сходства распознавания объекта (строки) со строками, принадлежность которых к заданным классам известна.
Проиллюстрируем описанный алгоритм распознавания на примере. Задано 10 классов объектов (рис. 4.2а). Требуется определить признаки таблицы обучения, пороги и построить оценки близости для классов объектов, показанных на рис. 4.2б. Предлагаются следующие признаки таблицы обучения:
x1- количество вертикальных линий минимального размера;
x2- количество горизонтальных линий;
x3- количество наклонных линий;
x4- количество горизонтальных линий снизу объекта.
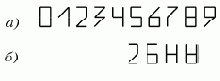
Рис. 4.2. Пример задачи по распознаванию
На рис. 4.3 приведена таблица обучения и пороги
?1=1, ?2=1, ?3=1, ?4=1,

Из этой таблицы видно, что неразличимость символов 6 и 9 привела к необходимости ввода еще одного признака x4.
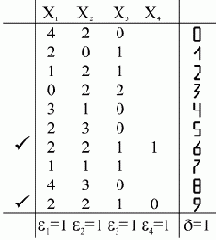
Рис. 4.3. Таблица обучения для задачи по распознаванию
Теперь может быть построена таблица распознавания для объектов на рис. 4.2б.
| Объект 1 | 1 | 2 | 1 | Цифра 2 | |
| Объект 2 | 3 | 3 | 0 | 1 | Цифра 8 или 5 |
| Объект 3 | 4 | 1 | 0 | ||
| Объект 4 | 4 | 2 | 0 | 1 |

Заключая данный раздел лекции, отметим важную мысль, высказанную А. Шамисом в работе [55]: качество распознавания во многом зависит от того, насколько удачно создан алфавит признаков, придуманный разработчиками системы. Поэтому признаки должны быть инвариантны к ориентации, размеру и вариациям формы объектов.
