Интеллектуальные робототехнические системы
       

Системы продукций


Под продукцией будем понимать выражение:

Если <X1, X2 ... Xn> то <{Y1, D1}, ... {Ym,Dm}>,

где: Xi,Yi - логические выражения, Di - фактор достоверности (0,1) или фактор уверенности (0,100).

Системы продукций - это набор правил, используемый как база знаний, поэтому его еще называют базой правил. В Стэндфордской теории фактор уверенности CF (certainty factor) принимает значения от +1 (максимум доверия к гипотезе) до -1 (минимум доверия).

А.Ньюэлл и Г.Саймон отмечали в GPS, что продукции соответствуют навыкам решения задач человеком в долгосрочной памяти человека. Подобно навыкам в долгосрочной памяти эти продукции не изменяются при работе системы. Они вызываются по "образцу" для решения данной специфической проблемы. Рабочая память продукционной системы соответствует краткосрочной памяти, или текущей области внимания человека. Содержание рабочей области после решения задачи не сохраняется.

Работа продукционной системы инициируется начальным описанием (состоянием) задачи. Из продукционного множества правил выбираются правила, пригодные для применения на очередном шаге. Эти правила создают так называемое конфликтное множество. Для выбора правил из конфликтного множества существуют стратегии разрешения конфликтов, которые могут быть и достаточно простыми, например, выбор первого правила, а могут быть и сложными эвристическими правилами. Продукционная модель в чистом виде не имеет механизма выхода из тупиковых состояний в процессе поиска. Она продолжает работать, пока не будут исчерпаны все допустимые продукции. Практические реализации продукционных систем содержат механизмы возврата в предыдущее состояние для управления алгоритмом поиска.

Рассмотрим пример использования продукционных систем для решения шахматной задачи хода конем в упрощенном варианте на доске размером 3 x 3 [2]. Требуется найти такую последовательность ходов конем, при которой он ставится на каждую клетку только один раз (рис. 2.2).

Записанные на рисунке предикаты move(x,y) составляют базу знаний (базу фактов) для задачи хода конем.
Продукционные правила - это факты перемещений move, первый параметр которых определяет условие, а второй параметр определяет действие (сделать ход в поле, в которое конь может перейти). Продукционное множество правил для такой задачи приведено ниже.

P1: If (конь в поле 1) then (ход конем в поле 8) P2: If (конь в поле 1) then (ход конем в поле 6) P3: If (конь в поле 2) then (ход конем в поле 9) P4: If (конь в поле 2) then (ход конем в поле 7) P5: If (конь в поле 3) then (ход конем в поле 4) P6: If (конь в поле 3) then (ход конем в поле 8) P7: If (конь в поле 4) then (ход конем в поле 9) P8: If (конь в поле 4) then (ход конем в поле 3) P9: If (конь в поле 6) then (ход конем в поле 1) P10: If (конь в поле 6) then (ход конем в поле 7) P11: If (конь в поле 7) then (ход конем в поле 2) P12: If (конь в поле 7) then (ход конем в поле 6) P13: If (конь в поле 8) then (ход конем в поле 3) P14: If (конь в поле 8) then (ход конем в поле 1) P15: If (конь в поле 9) then (ход конем в поле 2) P16: If (конь в поле 9) then (ход конем в поле 4)


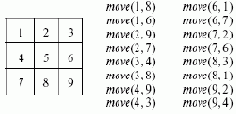
Рис. 2.2.  Шахматная доска 3х3 для задачи хода конем с допустимыми ходами

Допустим, необходимо из исходного состояния (поле 1) перейти в целевое состояние (поле 2). Итерации продукционной системы для этого случая игры показаны в таблице 2.1.

Таблица 2.1. Итерации для задачи хода конем№ итерацииТекущее полеЦелевое полеКонфликтное множествоАктивация правила
1121, 21
28213, 1413
3325, 65
4427, 87
59215, 1615
622

Выход
Продукционные системы могут порождать бесконечные циклы при поиске решения. В продукционной системе эти циклы особенно трудно определить, потому что правила могут активизироваться в любом порядке. Например, если в 4-й итерации выбирается правило 8, мы попадаем в поле 3 и зацикливаемся. Самая простая стратегия разрешения конфликтов сводится к тому, чтобы выбирать первое соответствующее перемещение, которое ведет в еще не посещаемое состояние. Следует также отметить, что конфликтное множество это простейшая база целей.В следующей лекции мы рассмотрим различные стратегии поиска в продукционных системах и пути разрешения конфликтов. В заключение данного раздела лекции перечислим основные преимущества продукционных систем:

  • простота и гибкость выделения знаний;
  • отделение знаний от программы поиска;
  • модульность продукционных правил (правила не могут "вызывать" другие правила);
  • возможность эвристического управления поиском;
  • возможность трассировки "цепочки рассуждений";
  • независимость от выбора языка программирования;
  • продукционные правила являются правдоподобной моделью решения задачи человеком.



Содержание раздела